Optimisation d’Algorithmes pour la Recherche de Carrés Maximaux avec des KD-Trees en Rust
Contexte du projet
L’objectif du projet est de trouver le meilleur carré possible dans un espace contenant des points bleus et rouges. Un carré est défini par ses coordonnées (x, y) dans le plan et sa taille est fixée à 100 unités de côté. Le but est de maximiser le nombre de points bleus à l’intérieur du carré tout en minimisant le nombre de points rouges.
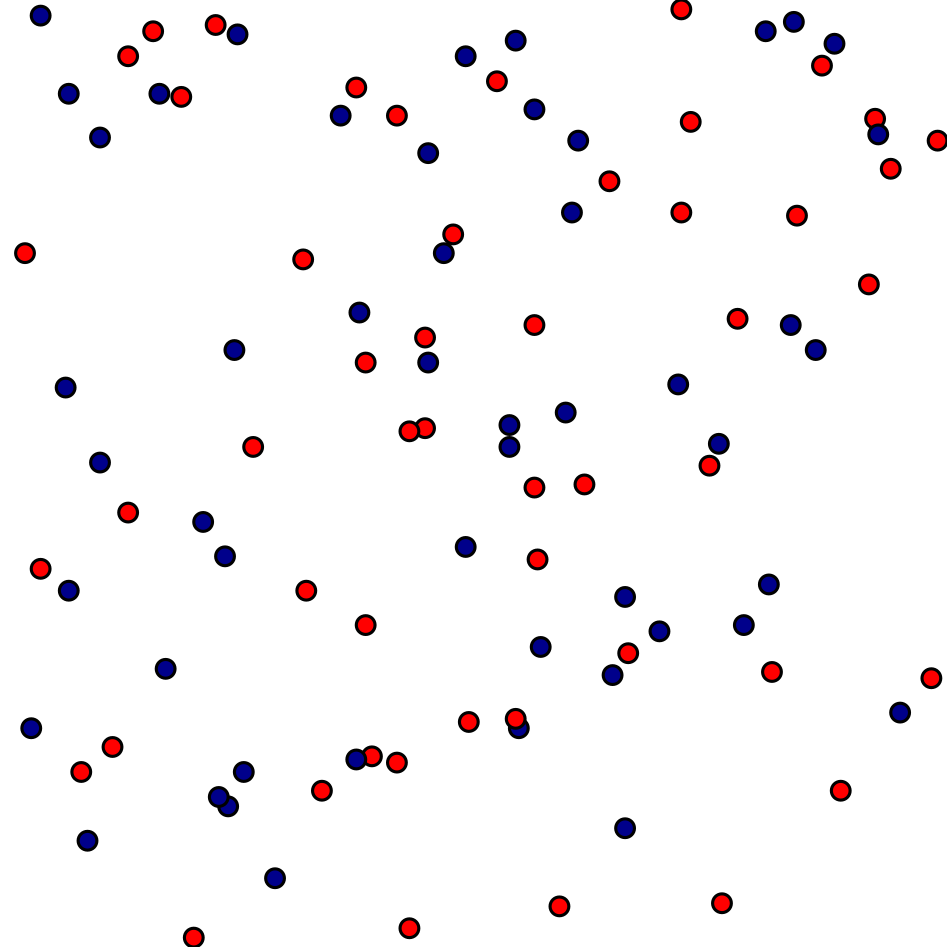
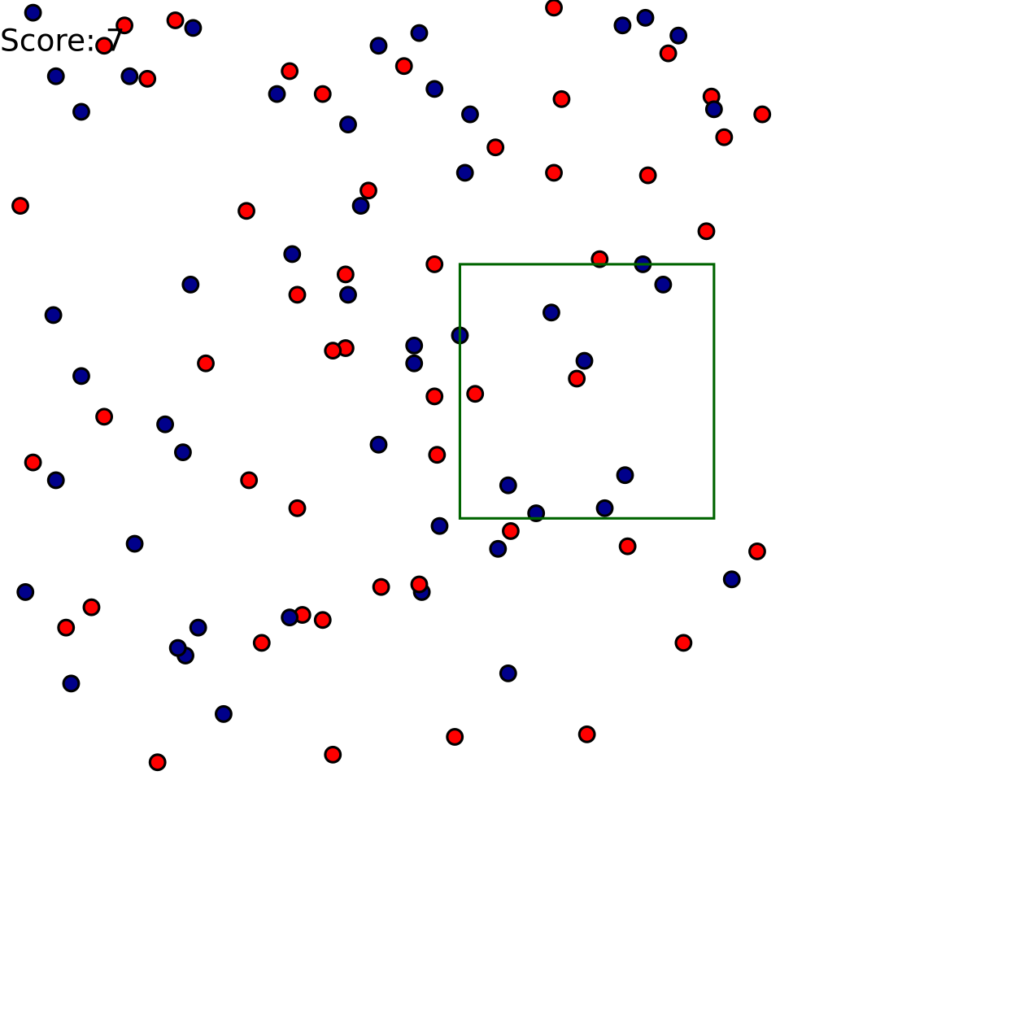
Pour cela, j’ai utilisé trois algorithmes distincts : un algorithme naïf, un algorithme utilisant les KD-trees et une version modifiée de cet algorithme avec des améliorations supplémentaires.
Structures de données
Le programme repose sur plusieurs structures de données et modules en Rust :
- SVG : Ce module permet de charger et de traiter les fichiers SVG d’entrée, dans lesquels les points sont définis. Les points sont triés et filtrés par couleur.
- Square : Une structure qui modélise un carré et permet de calculer son score, basé sur le nombre de points bleus et rouges à l’intérieur du carré.
- KD-tree : Une structure de données permettant de stocker et de rechercher des points efficacement en deux dimensions.
Algorithme naïf
L’algorithme naïf parcourt toutes les paires possibles de points bleus et rouges pour essayer de déterminer la meilleure position pour le carré.
Cet algorithme vérifie chaque paire de points bleus et tente de placer un carré. Chaque carré est évalué en calculant un score, qui est la différence entre les points bleus et les points rouges à l’intérieur. Bien que simple, cet algorithme est très lent pour des ensembles de données volumineux car il a une complexité en O(n²).
Algorithme KD-tree
Pour améliorer les performances, j’ai implémenté une version de l’algorithme utilisant un KD-tree, qui permet de rechercher les points dans un carré de manière plus efficace. Le KD-tree est une structure de données qui divise l’espace à chaque niveau, réduisant ainsi le nombre de comparaisons nécessaires pour les requêtes spatiales.
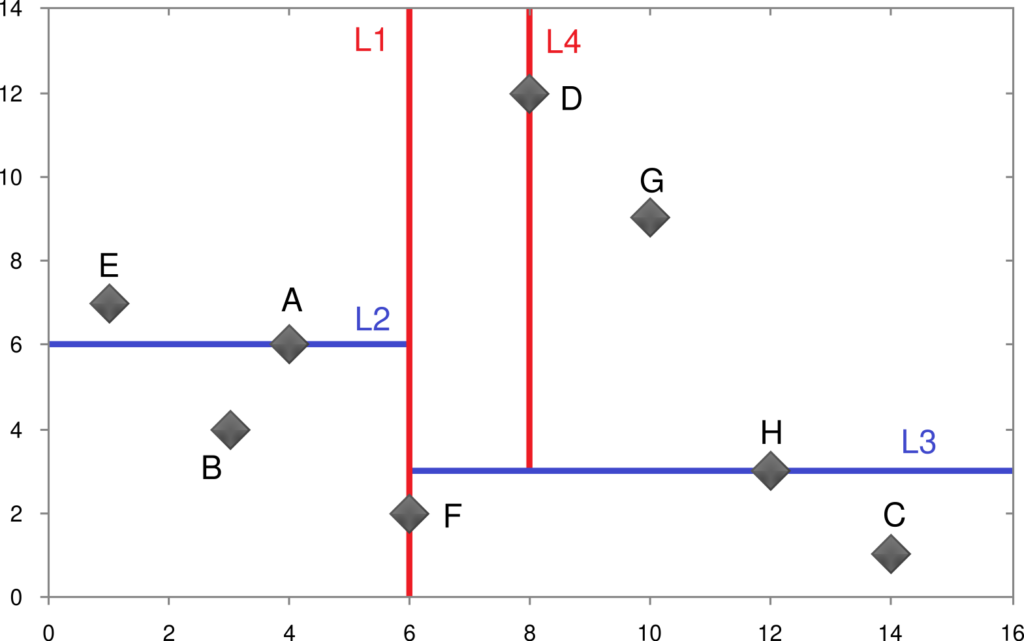
Cela permet de réduire considérablement le temps de calcul par rapport à la méthode naïve.
Algorithme KD-tree modifié
Dans cette version modifiée, j’ai ajouté une étape d’optimisation supplémentaire. Au lieu de vérifier toutes les paires de points, j’utilise une recherche par voisinage pour limiter le nombre de comparaisons. Cela permet d’améliorer davantage les performances, surtout lorsque les ensembles de points sont très dispersés.
Grâce à l’utilisation des recherches dans un rayon de proximité, cet algorithme réduit encore plus le nombre de carrés à évaluer. Cela rend l’algorithme particulièrement efficace pour les grandes instances de problèmes où les points sont distribués de manière irrégulière.
Comparaison des performances
Les trois algorithmes ont été testés avec différents ensembles de données et ont montré des performances très contrastées. L’algorithme naïf, bien que simple, devient rapidement inefficace dès que le nombre de points augmente. Le KD-tree apporte une amélioration significative, surtout pour les grandes instances, en réduisant la complexité des requêtes spatiales. Enfin, la version modifiée du KD-tree combine à la fois la puissance de la structure KD-tree et une réduction des comparaisons, ce qui en fait l’approche la plus rapide.
Résultats et visualisation
Chaque algorithme génère un fichier SVG en sortie, où le carré optimal est dessiné sur l’ensemble des points bleus et rouges.
Les temps d’exécutions sont les suivants :
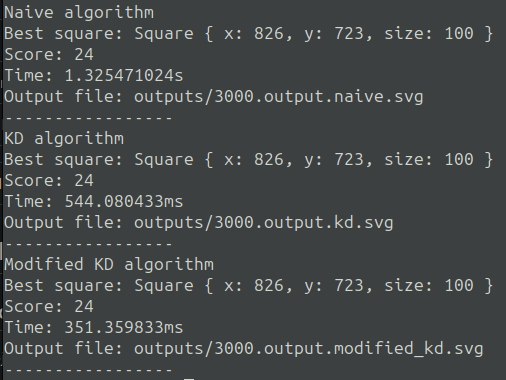
Conclusion
Ce projet m’a permis de renforcer mes compétences en Rust et d’approfondir mes connaissances sur les structures de données avancées comme les KD-trees. L’utilisation de ces arbres a permis d’optimiser un problème de recherche spatiale et de rendre l’algorithme beaucoup plus performant. Ce projet est un bon exemple d’optimisation algorithmique grâce à des structures de données adaptées.
Technologies utilisées :
- Langage : Rust
- Structure de données : KD-tree
- Format de visualisation : Fichier SVG
- Par Christophe Dang Ngoc Chan (Cdang (d)) — Travail personnel, inspired by File:KD-Tree part1.png by Alexandre Delesse (User:Prométhée33), CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=35134508 ↩︎